The formula for Series RC circuit with Phasor Diagram

Series RC circuit formula explanation

 R- the resistance -opposition to current flow (ohms)Ω

C- capacitance-opposition to any change in voltage ,farad(f)

 VR=IR- voltage drop of the resistor

Vc= q/c=∫idt/c- voltage drop in the capacitor

     

     When a capacitor and a resistor  are in series current will flow to charge the capacitor .

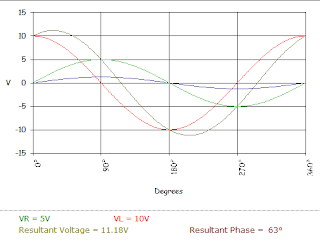
 The two voltages VR and VC cannot be added directly and the phasor diagram is used  to find the resultant or the applied voltage amplitude and phase angle . 

Voltage VC can be found using Ohms law where VC = XC x I

The resultant or applied voltage is that which or developed across the circuit with these particular component values.  The resultant voltage can be greater than the individual values of VR and Vc   

As this is capacitive circuit the resultant voltage angle will lag the current I

Current I is shown as being in phase with VR . VC will lag I by 90.

Series RC circuit Phasor Diagram

Series RC circuit Formula

Here are the Formulas and the proof solution for the formula in RC circuit:

Series RC circuit Waveform

This is an example of a waveform produced by the   resultant voltage and corresponding resultant phase  angle.

Analyze the formula for Series RL circuit and its Phasor Diagram

   Series RL circuit

R- the resistance -opposition to current flow (ohms)Ω

L- Inductance -opposition to any change  

XL- inductive resistance

VR=I R volts

VL=I XL volts

XL = inductance reactance  (ohms) Ω

      = 2πfL= ωL

Voltage developed across R and L cannot be added directly. The phasor diagram is used to show the resultant voltage and phase angle.The resultant or the applied voltage will lead the current I which is given an arbitrary value in the instance to show that is in phase with VR

Phasor diagram Series RL circuit:

Series RL circuit Formula :

Series RL Circuit generated Waveform:

The larger the relative value of the  XL to R the closer the resultant phase angle willl be 90 degrees which is an indication of the amount of inductance in the circuit.

Series and parallel resistance circuit :explanation

The familiarity of the few circuit building blocks is important in  understanding complex circuits. In this post I will explain the most important ideas in  DC circuits.

From my previous posts I discussed about the Ohms law . This is a continuation of the post about  simple direct current circuits. 

   

Resistors in series

   A series circuit is one in which total line current passes through each and every conductor in the circuit. two or more electric component are considered to be in series in the same current flows through all these component

laws of Series circuit

1. current in all parts of the series circuit is the same

It=I1+I2+I3+In

2. voltage across a group of conductor connected in series is equal to the sum of the individual voltage across individual resistors

Et=E1+E2+E3+En

3. total resistance of a group of conductors connected in series is equal to the sum of the individual resistances

Rt=R1=R2+R3+Rn

Resistors in parallel

  A parallel circuit is one in which current may flow through two or more independent branches.Two or more components are considered in parallel if the same voltage appears across all these components

laws of parallel circuits

1. total voltage of a parallel circuit is the same as across each branch of circuit

Et= E1=E2=E3=En

2.Total current is equal to the sum of individual branch currents

It=I1+I2+I3+In

3.The reciprocal of the total resistance of a number of resistors connected in parallel is equal to the sum of the reciprocals of the separate resistances.Total resistance is always less or approximately equal to the values of the smallest resistive branch

1/Rt=1/R1+1/R2+1/R3+1/Rn
 Rt=1/(1/R1+1/R2+1/R3+1/Rn)

Note that : it is important to know that connecting additional resistors in series increases resistance, while connecting additional resistance in parallel decreases the total resistance.