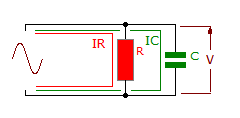
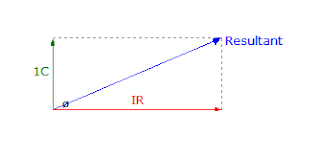
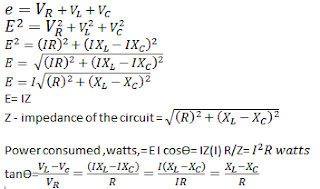Power Factor for a more efficient circuit and loading

Power factor is an important aspect to consider in AC circuit, because any factor less than 1 means that the circuit wiring has to carry more current than what would be necessary with zero reactance in the circuit to deliver the same true power to the resistive load.
    When expressed as fraction, the ratio between true power and  apparent power is called the power factor of the circuit.
                                                     Kw
The power factor is given cosƟ = --------
                                                    KVA
in the case of single phase supply

                     VI                    KVAx1000
KVA=     ----------  or I=    -----------  
                     1000                    V

In case of three-phase supply
            sqrt(3)VL IL                 KVAx 1000
KVA= --------------     or IL=-------------
                1000                           sqrt(3)VL
In the case of three phase supply
   All current will cause losses in the supply and distribution system. A load with a power of 1.0 result in the most efficient loading of the supply and a load with a power of 0.5 will result in much higher losses in the supply such as an induction motor, power transformer, lighting ballast,welder or variable speed drive, switched mode power supply, discharge lighting or other electronic load.
  The heating and lighting loads supplied from three-phase supply have power factors ranging from 0.95 to unity. But motor loads have usually low lagging power factor ranging from 0.5 to 0.9. Single phase motors may have a power factor of as low as 0.4 and electric welding units have even lower power factor of 0.2 or 0.3
 A poor power factor due to an inductive load can be improved by the addition of power factor correction,but a poor power factor due to a distorted current waveform requires a change in equipment design or expensive harmonic filter s to gain an appreciable improvement. many inverters are quoted as having a power factor of better than 0.95 when in reality, true power factor is between 0.5 and 0.75. the Figure of 0.95 is based on the cosine of the angle between the voltage and current but does not take into account that the current waveform is discontinues and therefore contributes to increased losses on the supply
   in each  equation above, the KVA is directly proportional to the current. The chief disadvantage of a low power factor is that the current requires for a given power is very high. this fact leads to the following undesirable results.

1. Large KVA for a given amount of power.
    All electric machines such as alternators, transformers, cables are limited in their current-carrying capacity by the permissible temperature rise which is proportional to I^2 .hence, they may all be fully loaded with respect to their rated KVA without delivering their full power.

2. Poor voltage regulation . When loading a low lagging power factor is switched on,there is a large voltage drop in the supply lines and transformers. this drop in voltage adversely affects the starting torque of motors and needs expensive voltage stabilizing equipment for keeping the consumers voltage fluctuations within the statutory limits

RLC parallel circuit formula and Phasor diagram

RLC in parallel

RCL parallel circuit can be considered as two reactance's XC and XL where the currents are in phase opposition in parallel with the resistor.

Through the use of  the phasor diagram the effective total resistance can be found  . It can be observed that IR is at the base of the right triangle and IL minus IC minus IL forming the perpendicular.

The amplitude of the resultant current is the hypotenuse.

To calculate the resultant we use the Pythagorean theorem . Ic and IL  are 180 degree out of phase  therefore cancel out. The resultant current is the difference between the two.

              

Impedance  phase angle  is calculated from the difference between IL and IC divided by IR

Parallel RC circuit formula and phasor diagram

RC circuit in parallel formula and diagram

Currents in IR and IC are 90 degree out of phase and cannot be added directly. The total current or resultant will depend upon the resistance and R and the reactance ( AC reactance) of AC

Parallel RC circuit Phasor diagram :

As the reactance of C falls relative to resistance of R , so more current flows in the capacitor branch and the resultant phase angle increases

Parallel RC circuit formula :

Parallel RL circuits formula and Phasor diagram explanation

Parallel  RL circuit formula and diagram

The current through L will lag  IR  by 90 degrees . The resultant negative phase angle  depends upon the relative values of R and XL. for R, E and R in phase . For  XL , E and IL in quadratic lagging current.

As  the circuit is inductive the phase angle is  negative.

Parallel RL circuit Phasor Diagram

There cannot be a direct addition of IR and IL because of their 90 degree phase angle. 

Parallel RL circuits formula

Series RLC circuit formula explanation

Series RLC circuit diagram and formula

Resistance ,inductance capacitance in series

  

In RLC series circuit , the series current is common for Resistance, Capacitance and inductance . VR will be in phase width I. Whereas the voltage of Vc and VL will be 180 degree phase opposition, resulting in some cancellation.

Series RLC  Phasor Diagram

The phasor diagram will produce the resultant circuit voltage and its phase angle. Positive angle indicate a greater inductive circuit influence and negative angle capacitive.

This is the corresponding formula for RLC circuit

Series RLC Formulas