Electronics :Traffic light Circuit

This is a two way continuous traffic light circuit which uses  LED, diodes and IC's . 

Usually most traffic light in the world is PLC controlled but this circuit is  simple  and easy to build . 

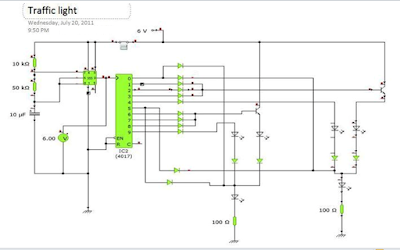
 In the image below is the schematic diagram of the project . I used Yenka Free Software to simulate and see if its properly working . You can download it free on Yenka website.

The  clock pulses from the 555 astable circuit is sent into the 4017 decade counter . Each output becomes high in turn as the clock pulses are received. Appropriate outputs are combined with diodes to supply the amber and green LEDs. 

components :

• resistors: ,50k ohm, 10k ohm, two-100k ohm
• capacitors: 10µF 16V radial
• diodes:  16 pieces of 1N4148 
• LEDs: 2 sets of ( red, amber or yellow, green)
• IC:555 timer ,  4017 counter
•  on/off switch

You can adjust the timing of light-shifting by adjusting the  value of the resistor in the astable circuit . 

Plane Geometry Review : Triangle Area calculation

Area Formulas

1.  Given base and altitude

Triangle: Given base and height

Area = 1/2 (b)(h)

2. Given two sides and an Angle

 Triangle:  Given 2 sides and angle

Area = 1/2 (a) (b)sin θ

3. Given 3 sides

Triangle Given 3 sides a,b,c

Area = sqrt (s(s-a)(s-b)(s-c))----->  Heron's Formula  

where s= (a+b+c)/2

4. Triangle inscribed in a circle

r= radius of the circle 

Area = (a b c)/ 4r

5. Given a circle inscribed in a Triangle

r = radius of the circle

Area  =  rs 

s = ( a+b+c/) 2

6. Circle escribed by the triangle

where a is the side tangent to the circle

Area =  r (s-a)

s = ( a+b+c/) 2

Engineering Mathematics : Plane Geometry Part 1

Fundamental Principles


Angles

• Acute angle = less 90 deg
• Obtuse angle = more than 90 and less than 180 deg
• Straight angle =180 deg
• Vertex of the angle is point where two lines meet
• Supplementary angles have a sum of 180 deg
• Complementary angles have a sum of 90 deg
• The base angles of an isosceles (two equal sides) triangle =  60 deg
• Each angle of an isosceles right triangle = 45 deg
• Exterior angle of a triangle is the sum of the remote interior angle
• The sum of the angles of a polygon of n sides = (n-2)180 deg
• The sum of the exterior angles of any polygon = 360 deg

Congruence of triangle

In geometry,Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in size

conditions:   (s=side  ; a=angle)

• s.a.s =s.a.s   (Side-Angle-Side)
• a.s.a=a.s.a  (Angle-Side-Angle)
• s.s.s=s.s.s  (Side-Side-Side
• a.a.s=a.a.s (Angle-Angle-Side)

Two right triangles are congruent if hypotenuse and leg of one hypotenuse and corresponding leg of the other.

Algebra: What are the examples of Empirical formula

Some Formulas are derived by means of experimentation. Among these are the formulas discovered by pascal, Galileo and Archimedes. They are called empirical formulas.

Examples of Empirical formulas:
1.1 a formula for changing temperature from Fahrenheit to centigrade.

2.   a formula showing the relation of weights on a balance with the lengths of its arms.

3. -a formula used in finding electrical power.

4.a formula for finding work done in foot pounds.

5. an ohms law, a formula for finding I, the number of amperes of electric current , E, the electromotive force in volts, and R, the resistance in ohms.

6. a formula for finding the distance covered by falling bodies.

Algebra: What is the Lowest common Multiple in Algebraic Expression

The lowest common multiple ( L.C.M) of two or more arithmetical or algebraic expressions is the expression having the least number of factors which  will exactly contain each of the iven expressions.Thus the numbers 4, 6 and 12 will have 12 for their LCM for it exactly contains each of the numbers. it is easier  to find the LCM  of the polynomials like   and

         
  We find that,  while

Therefore, the LCM of the polynomials is

Note:
To find the LCM of two or more expressions, separate each expression into its prime factors. Then take the product of all the different prime factors using each factor the greatest number of times it occurs in any one expression