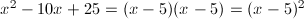Algebra: How to factor a trinomial Perfect Square

From your previous topics , You learned that the square of a binomial is a trinomial perfect square. Thus , the factors of a trinomial perfect square are two binomials which may be written as the square of a binomial.

To illustrate this point , let us consider the following examples.
Example.1
Multiplication

factoring

 is the square root of  
while 3 is the square root of 9


Example 2
Multiplication

factoring

  is the square root of 
while 5 is the square root of 25


Note:
From the examples , it is clear that the following points should be noted in factoring a trinomial perfect square.
1.The factors consists pf like binomials whose terms are the square roots of the terms which are perfect squares.
2. The sign connecting the terms of the binomial factor is the same as the sign of the remaining term.


Hence if a trinomial is perfect square, its factors can be easily be determined.
The problem then is , " How do we know that a trinomial is a perfect square?"


let us consider the trinomial 

Analysis: 

or

and

or

 therefore 

and 9 are perfect squares . 2x is called the square root of 

 and 3 is the square root of 9. Now   

and if their product is doubled , we get  

which is the middle term of the trinomial.

Therefore, trinomial is a perfect square if the following conditions exist:
1. Two terms are positive perfect squares.
2. The third term (generally the middle term) is twice the product of the square roots of the terms which are perfect and may be either positive or negative.

Algebra: How to Translate verbal Statements into symbols

An equation is an important tool in problem solving but another tool which is just as necessary is representing related quantities by means of symbols. It must be recalled thatb letter like x can be used to represent the numerical value of a certain quantity. quantities related to the latter may also be expressed in terms of x . For example , if x represents the first of two consecutive integers, then the next consecutive integer( which is greater by 1) will be represented by x+1.

 There are certain rules which must be followed in representing quantities. generally, it is sufficient to use x or any chosen symbol to represent the smaller of two quantities or the smallest of three or more quantities. another way is by representing the independent quantity by x. suppose , for example, that Pedro is twice as old as Juan. this condition shows that the age of Pedro depends upon the age of Juan and hence it is better to let x represent the age in years of Juan. Pedro's age in years will re represented by 2x

Algebra: What is mean Proportion and How to solve it?

A proportion such as 1:2 =2:4 or a:b = b:c  is called a mean proportion because the second and the third terms are equal. In the latter b is the mean proportional between the first and the last terms a and c, respectively and c is the third proportional to a and b.

Solving for the mean proportional
 Given
 in proportion, the product of the extremes is equal to the product of the means.
  extracting the square roots of booth members of the equation

Note; like roots and like powers of equal numbers are equal

It follows that:
The mean proportional between two quantities is equal to the square root of their product.

example 1 :
Solve for x in

example 2 :
Solve for x in

Algebra: How to solve the Equations containing decimals

Equations containing decimals are equations with fractions. hence the solution of decimal equations is similar to that of fractional equations with this difference-in decimal equation the multiplier of both members is that power
of ten that will clear the equations of its decimal.

Example1.
Solve for x:                                 .3x + 5 = .2x
Multiplying both members          
of the equation by 10,                 3x + 50 = 2x
                                                  x = -50

Check                                     .3x(-50) + 5 = .2(-50)
                                              -15+5  = -10
                                               -10 = -10

Example no 2.                                      Solve for y in the equation
                                                         .5y/3 - .18/4 = .1y/6
Clear the equation of decimals by multiplying both members by 100
50y/3 - 18/4 = 10y/6
Clear the equation of fractions by multiplying both members by 12, the LCD
200y - 54 = 20y
180y = 54
y = 54/180 = .3

check:
.5y/3 - .18/4 = .1y/6
(.5(.3))/3 -.18/4  = (.1(.3))/6
.05-.045 = 0.005
.005 = .005



                                            

Algebra : How to solve a Literal equation

Equations where the known quantities are expressed as letters are called literal equations. Formulas are literal equations. Generally, the last letter of the alphabet are used to represent the unknown quantities, and the first letters, the known quantities.

Examples:

Solve for the unknown and check

1. 3x + 2a = 2x+5a     transposing
    3x - 2x = 5a - 2a      combining like terms
           x = 3a  


check
3.3a + 2a = 2.3a + 5a
9a + 2a = 6a + 5a
11a = 11a


2. 8z + 6m = 5z + 9m
    8z - 5z = 9m - 6m        transposing
    3z = 3m                   combining like terms
    z = m                       axiom of division

check
   8.m + 6m = 5.m + 9.m
   8m + 6m= 5m + 9m
   14m = 14m