From your previous topics , You learned that the square of a binomial is a trinomial perfect square. Thus , the factors of a trinomial perfect square are two binomials which may be written as the square of a binomial.
To illustrate this point , let us consider the following examples.
Example.1
Multiplication
factoring
 is the square root of
is the square root of  while 3 is the square root of 9
while 3 is the square root of 9Example 2
Multiplication
factoring
 is the square root of
is the square root of  while 5 is the square root of 25
while 5 is the square root of 25Note:
From the examples , it is clear that the following points should be noted in factoring a trinomial perfect square.
1.The factors consists pf like binomials whose terms are the square roots of the terms which are perfect squares.
2. The sign connecting the terms of the binomial factor is the same as the sign of the remaining term.
Hence if a trinomial is perfect square, its factors can be easily be determined.
The problem then is , " How do we know that a trinomial is a perfect square?"
let us consider the trinomial
Analysis:
therefore

and 9 are perfect squares . 2x is called the square root of

and 3 is the square root of 9. Now
and if their product is doubled , we get
which is the middle term of the trinomial.
Therefore, trinomial is a perfect square if the following conditions exist:1. Two terms are positive perfect squares.
2. The third term (generally the middle term) is twice the product of the square roots of the terms which are perfect and may be either positive or negative.



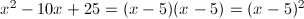







0 comments:
Post a Comment
please leave a comment of what do you think about this article.