Complex number review
Complex number are usually discussed in the first part of advanced mathematics and here is a quick review about it.
Consider the equation
it has has NO SOLUTION in real number system.

But in eighteenth century mathematician invented a new number "i" which is defined by the property. this in turn , led to the development of complex numbers, which are numbers of the form a+bi .
"a "and "b" are real numbers. But it can be also observed that every real number a is also a complex number because it can be written as a=a+0i. Thus ,the real numbers are a subset of the complex numbers.
With these properties complex number can be now defined as.
---the combination of real and imaginary number which can be expressed in the form a+bi or a+jb where i or j=-1
Powers of i or j
Note for j^n
If n is divided by 4 and the result is 1 it follows j^4. if the result has a decimal value of (.75) if follows j^3.If (.50) it follows j^2. If (.25) it follows j
Argand's diagram
real axis
Forms of complex numbers -complex number can be expressed in different notations.
1.) rectangularr form -complex number is denoted by its respective horizontal and vertical components.
a+jb where: a-real value
jb-imaginary axis
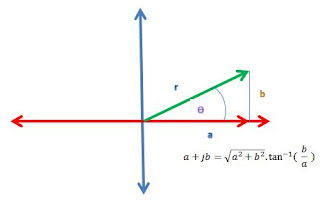
2.) polar form - complex number can be denoted by the length and the angle of its vector
r∠Ɵ where: r- magnitude
Ɵ - argument,degrees
3.) trigonometric form
rcosƟ +jsinƟ where: r-magnitude
Ɵ-argument,degrees
4.) Exponential form
where: r-magnitude
Complex number are usually discussed in the first part of advanced mathematics and here is a quick review about it.
Consider the equation
it has has NO SOLUTION in real number system.

But in eighteenth century mathematician invented a new number "i" which is defined by the property. this in turn , led to the development of complex numbers, which are numbers of the form a+bi .
"a "and "b" are real numbers. But it can be also observed that every real number a is also a complex number because it can be written as a=a+0i. Thus ,the real numbers are a subset of the complex numbers.
With these properties complex number can be now defined as.
---the combination of real and imaginary number which can be expressed in the form a+bi or a+jb where i or j=-1
Powers of i or j
Note for j^n
If n is divided by 4 and the result is 1 it follows j^4. if the result has a decimal value of (.75) if follows j^3.If (.50) it follows j^2. If (.25) it follows j
Argand's diagram
real axis
Forms of complex numbers -complex number can be expressed in different notations.
1.) rectangularr form -complex number is denoted by its respective horizontal and vertical components.
a+jb where: a-real value
jb-imaginary axis
2.) polar form - complex number can be denoted by the length and the angle of its vector
r∠Ɵ where: r- magnitude
Ɵ - argument,degrees
3.) trigonometric form
rcosƟ +jsinƟ where: r-magnitude
Ɵ-argument,degrees
4.) Exponential form
where: r-magnitude
Ɵ-argument,degrees