Plane Geometry Review : Triangle Area calculation

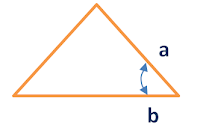
Area Formulas

1.  Given base and altitude

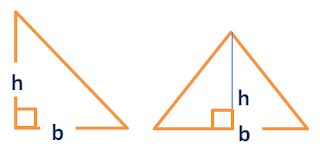Triangle: Given base and height

Area = 1/2 (b)(h)

2. Given two sides and an Angle

 Triangle:  Given 2 sides and angle

Area = 1/2 (a) (b)sin θ

3. Given 3 sides

Triangle Given 3 sides a,b,c

Area = sqrt (s(s-a)(s-b)(s-c))----->  Heron's Formula  

where s= (a+b+c)/2

4. Triangle inscribed in a circle

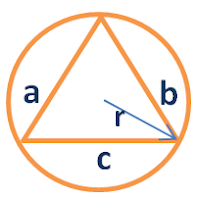r= radius of the circle 

Area = (a b c)/ 4r

5. Given a circle inscribed in a Triangle

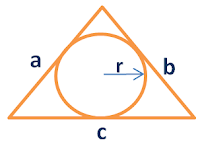r = radius of the circle

Area  =  rs 

s = ( a+b+c/) 2

6. Circle escribed by the triangle

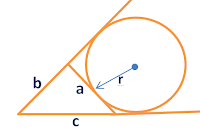where a is the side tangent to the circle

Area =  r (s-a)

s = ( a+b+c/) 2

Engineering Mathematics : Plane Geometry Part 1

Fundamental Principles


Angles

• Acute angle = less 90 deg
• Obtuse angle = more than 90 and less than 180 deg
• Straight angle =180 deg
• Vertex of the angle is point where two lines meet
• Supplementary angles have a sum of 180 deg
• Complementary angles have a sum of 90 deg
• The base angles of an isosceles (two equal sides) triangle =  60 deg
• Each angle of an isosceles right triangle = 45 deg
• Exterior angle of a triangle is the sum of the remote interior angle
• The sum of the angles of a polygon of n sides = (n-2)180 deg
• The sum of the exterior angles of any polygon = 360 deg

Congruence of triangle

In geometry,Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in size

conditions:   (s=side  ; a=angle)

• s.a.s =s.a.s   (Side-Angle-Side)
• a.s.a=a.s.a  (Angle-Side-Angle)
• s.s.s=s.s.s  (Side-Side-Side
• a.a.s=a.a.s (Angle-Angle-Side)

Two right triangles are congruent if hypotenuse and leg of one hypotenuse and corresponding leg of the other.